Alek Oktadinata

1. UKURAN NILAI PUSAT

Ukuran pemusatan adalah sembarang ukuran yang menunjukkan pusat segugus data yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya

1. Data yang tidak dikelompokkan

Adalah data yang berdiri sendiri secara numerik berdasarkan data apa adanya.

1. Mean

Mean atau rata-rata merupakan hasil bagi dari sejumlah skor dengan banyaknya responden. Perhitungan mean merupakan perhitungan yang sederhana karena hanya membutuhkan jumlah skor dan jumlah responden (n). Jika pencaran skor berdistribusi normal, maka rata-rata skor merupakan nilai tengah dari distribusi frekuensi skor tersebut. Rata-rata tidak mempertimbangkan pencaran (variabilitas) skor, sehingga sebelum melakukan interpretasi atas nilai rata-rata perlu melihat variabilitasnya.

Cara Mencari Mean

Untuk data tunggal

untuk data berkelompok

x : rata-rata hitung populasi

xi            : data ke-I (untuk data tunggal)

xi            : nilai tengah (untuk data kelompok)

f             : banyak data

Sedangkan mencari mean untuk data interval menggunakan rumus:

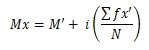
Mx = Mean

Mʹ = Mean Terkaan atau Mean Taksiran

i = Interval Kelas

Σfxʹ = jumlah perkalian titik tengah buatan sendiri dengan frekuensi dari masing-masing interval

N = Banyak Sampel

 

1. Median

Median merupakan skor yang membagi distribusi frekuensi menjadi dua sama besar. Langkah awal menentukan median adalah menyusun data menjadi bentuk tersusun menurut besarnya. Baru kemudian ditentukan nilai tengahnya (skor yang membagi distribusi menjadi dua sama besar). Jika jumlah frekuensi ganjil, maka nementukan median akan mudah yaitu skor yang terletak di tengah-tengah barisan skor. Apabila jumlah frekuensi genap, maka median merupakan rata-rata dari dua skor yang paling dekat dengan median. Median merupakan segugus data yang telah diurutkan dari yang terkecil sampai terbesar atau terbesar sampai terkecil yang tepat ditengah-tengahnya bila pengamatan itu ganjil, atau rata-rata kedua pengamatan yang ditengah bila pengamatannya genap maka:

Jika banyak data (n) ganjil dan tersortir, maka:

Jika banyak data (n) genap dan tersortir, maka:

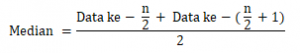
Untuk data interval menggunakan Rumus:

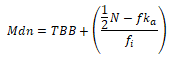
Mdn    = median

TBB    = low limit atau Tepi batas bawah

fi          = frekuensi kelas median

fk_a          = frekuensi kumulatif yang terletak diatas interval yang mengandung median

N         = banyak data

1. Modus

Merupakan nilai yang paling sering muncul atau dengan frekuensi yang paling tinggi. Modus tidak selalu ada, ini terjadi jika frekuensi semua data sama. Modus juga dapat lebih dari satu, jika terdapat lebih dari satu frekuensi tertinggi yang sama dan dikatakan sebagai bimodus.

Untuk menentukan modus dengan data interval

M_o       = Modus

TBB    = low lomit atau tepi batas bawah

fk_a          = frekuensi kumulatif yang terletak di atas interval yang mengandung modus

fk_b         = frekuensi kumulatif yang terletak di bawah interval yang mengandung modus

UKURAN LETAK

Individu skor atau nilai X disebut dengan raw score. Raw Score tidak dapat memberi informasi yang banyak, untuk itu perlu suatu perhitungan yang akan bermanfaat dalam menginterpretasikan skor yang terkumpul. Suatu contoh Nilai Praktek Lapangan mahasiswa A adalah 70, dalam hal ini si A tidak dapat mengatakan apa-apa tentang nilainya kecuali hanya menyebutkan besarnya nilai. Untuk mengevaluasi skor tersebut perlu banyak informasi seperti rata-rata kelas atau berapa banyak teman-temannya yang memperoleh nilai di bawahnya, sama dengannya, maupun di atasnya.

Frekuensi distribusi dapat dikelompok-kelompokkan menjadi beberapa bagian yang sama besar, pengelompokkan tersebut dapat dilakukan dengan : Quartile, Decile, dan Precentile.

1. Kuartil

Kuartil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 4 bagian yang sama besar.

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Kuartil ke-1 = n/4

Letak Kuartil ke-2 =  2n/4 = n/2 =  Letak Median

Letak Kuartil ke-3 = 3n/4

Dimana :

n                               : banyak data

Kelas Kuartil ke-q   : Kelas di mana Kuartil ke-q berada

Kelas Kuartil ke-q didapatkan dengan membandingkan Letak Kuartil ke-q dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

q          : 1,2 dan 3

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sebelum kelas Kuartil ke-q

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Kuartil ke-q

i           : interval kelas

f q        : Frekuensi kelas Kuartil ke-q

 

2. Desil

Desil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 10 bagian yang sama besar

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Desil ke-1 = n/10

Letak Desil ke-5 = 5n/10 = n/2 = Letak Median

Letak Desil ke-9 = 9n/10

Dimana:

n                      : banyak data

Kelas Desil ke-d          : Kelas di mana Desil ke-d berada

Kelas Desil ke-d didapatkan dengan membandingkan Letak Desil ke-d dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

d          : 1-9

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Desil ke-d dengan Frekuensi Kumulatif sebelum kelas Desil ke-d

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Desil ke-d

p          : panjang interval

f d        : Frekuensi kelas Desil ke-d

 

3. Persentil

Persentil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 100 bagian yang sama besar

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Persentil ke-1 = n/100

Letak Persentil ke-50 = 50n/100 = n/2 =  Letak Median

Letak Persentil ke-99 = 99n/100

Dimana:

n                      : banyak data

Kelas Persentil ke-p     : Kelas di mana Persentil ke-p berada

Kelas Persentil ke-p didapatkan dengan membandingkan Letak Persentil ke-p dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

p          : 1-99

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sebelum kelas Persentil ke-p

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Persentil ke-p

i           : interval kelas

f q        : Frekuensi kelas Kuartil ke-q

 

 

Silahkan tinggalkan pertanyaan pada menu “coment”

penerapan media blog dalam perkuliahan