Alek Oktadinata

Pengujian homogenitas varians adalah suatu teknik analisis untuk menguji apakah data berasal dari populasi yang homogeny atau tidak. Untuk menguji homogenitas varians terhadap dua kelompok sampel dapat dilakukan dengan uji F, sedangkan untuk menguji homogenitas varians terhadap tiga kelompok sampel atau lebih dapat dilakukan dengan uji Barlett.

Langkah pengujian homogenitas varians dua kelompok sampel (uji F)

• Hitung varians masing-msing kelompok data.
• Hitung hasil bagi antara varians yang besar dengan varians yang kecil

• Bandingkan F_hitung dengan F_tabel dengan menggunakan derajat kebebasn (n1-1), (n2-1) dengan kriterian sebagai berikut

Jika F_hitung lebih besar dari F_tabel berarti kelompok sampel memiliki varians tidak homogen

Jika F_hitung lebih kecil dari F_tabel berarti kelompok sampel memiliki varians yang homogen

Langkah pengujian hogenitas varians tiga kelompok sampel atau lebih (uji Barlett)

• Buat daftar/table mengenai besaran-besaran yang diperlukan untuk uji Barlett
• Varians gabungan dari semua sampel dengan rumus :

s²={ Σ ( ni-1 ) si² / (Σ ( ni-1 ) }

• Nilai satuan Barlett dengan rumus

B = (logs²). Σ (ni-1)

• Nilai satuan χ² dengan rumus

χ²_hitung  = (ln10) {B – Σ (ni-1) logs²}

• Bandingkan χ²_hitung dengan χ²_tabel  dengan kriterian sebagai berikut:

Jika χ²_hitung lebih besar dari χ²_tabel berarti kelompok sampel memiliki varians tidak homogen

Jika χ²_hitung lebih kecil dari χ²_tabel berarti kelompok sampel memiliki varians yang homogen

 

            Contoh aplikasi Uji Barlett

Dengan varians masing-masing kelompok sampel sebagai berikut: 

s₁²= 29,3           s₂²= 21,5          s₃²= 35,7          s₄²= 20,7

masukkan angka ke dalam table

•  Hitung varians gabungan dari empat sampel

Log s² = log 26,6 = 1,4249

• Hitung harga satuan Barlett

B = (logs²). Σ (ni-1)

B = (1,4249).  (14)

B = 19,9486

• Hitung nila χ²_hitung

χ²_hitung  = (ln10) {B – Σ (ni-1) logs²}

χ²_hitung  = (2,3026) {19,9486 – 19,8033}

χ²_hitung  = 0,3346

• Lihat nilai χ²_tabel
• Jika α=0,05, dari daftar distribusi chi kuadrat dengan dk = 3 (k-1) didapat harga χ²_{tabel(0,95)(3)}=7,81 karena χ²_hitung < dari χ²_tabel (0,3346 < 7,81) berarti data diperoleh dari populasi yang homogen.

Pengujian normalitas adalah suatu analisis yang dilakukan untuk menguji apakah data berasal dari populasi yang berasal dari populasi yang berditribusi normal atau tidak.

Pengujian normalitas menjadi penting karena kebanyakan analisis statistic yang bersifat inferential mensyaratkan bahwa data yang akan diolah seyogyanya berdistribusi normal.

Pengujian normalitas untuk data tunggal dapat dilakukan dengan uji lilliefors, sedangkan untuk data bergolong dapat dilakukan dengan chi kuadrat.

Uji Lilliefors

pengujian normalitas distribusi dengan uji Lilliefors pada umumnya digunakan untuk data tunggal. Adapun langkah-langkah uji normalitas lilliefors adalah sebagai berikut:

Langkah-langkah melakukan uji normalitas melalui uji Liliefors

• Susun data secara berurutan dari skor terkecil sampai skor terbesar
• Hitung rata-rata dan standar deviasi
• Hitunglah nilai standar baku dengan menggunakan z-skor dari masing-masing data
• Tentukan nilai normal standar baku (z-skor) dengan menggunakan table normal standar (baku) dari 0 – z.
• Tentukan peluang F(zi)

Catatan jika

zi (+) maka F(zi) = 0,5 + angka table (table normal standar (baku) dari 0 – z)

zi ( – ) maka F(zi) = 0,5 – angka table (table normal standar (baku) dari 0 – z)

• Tentukan nilai S(zi) dengan cara menghitung porporsi z1, z2, …zn yang lebih kecil atau sama dengan zi dengan rumus:
• 
• Hitung selisih harga mutlak F(zi) – S(zi)
• Ambil harga mutlak terbesar diantara harga mutlak tersebut dengan symbol Lo (Lilliefors Observasi
• Tentukan nilai L _table dengan menggunakan table liliefors (L_{tabel (0,05a),(n)}) dengan kiteria pembilang α = 0,05 dan penyebut = n
• Bandingkan Lo dengan Ltabel dengan kriterian sebagai berikut:

 

Jika Lo lebih besar dari Ltabel berarti populasi berdistribusi tidak normal

Jika Lo lebih kecil dari Ltabel berarti populasi berdistribusi normal

contoh soal:

diperoleh data sebagai berikut:

17, 16, 17, 19, 15, 15

setelah dianalaisis diperoleh rata-rata = 16,5 dan standar deviasi =1,52

kemudian dibuat tabel bantu uji normalitas Liliefors

Berdasarkan hasil analisis contoh data di atas maka dapat Lo = 0,204 dan (L_{tabel (0,05a),(n)}) = 0,319

Maka dapat disimpulkan bahwa data pada table diatas memiliki populasi berdistribusi normal karena Lo < Ltabel

 

UKURAN PENYEBARAN

Ragam dan Simpangan Baku untuk Data tidak Dikelompokkan

• Simpangan baku, paling sering digunakan untuk mengukur penyebaran. Nilai simpangan baku menunjukkan seberapa dekat nilai-nilai suatu data dengan nilai rata-rata.
• Nilai simpangan baku yang kecil → data menyebar dalam range lebih kecil mendekati nilai rata-rata mean, dan begitu sebaliknya.
• Nilai simpangan baku diperoleh dari akar kuadrat nilai ragam (varians)
• Ragam dari suatu data populasi dinotasikan sebagai σ², sedangkan untuk data sampel dinotasikan sebagai s².
• Simpangan baku σ (untuk data populasi), dan simpangan baku s (untuk data sampel)

adapun rumus standar Deviasi

Deviasi standar dan mean merupakan ukuran statistik yang memiliki reliabilitas yang tinggi sehinga dapat digunakan sbagai alat untuk evaluasi. Sebagai contoh dalam dunia pendididkan dapat digunaka sebagai alat evaluasi hasil belajar anak peserta didik. Cara yang sering digunakan sebagai bahan evalausi adalah sebagai berikut;

• Untuk menetapkan Nilai Batas Lulus Aktual (Minimum Passing Level atau Passing Grade), nilai yang digunakan sebagai acuan untuk keperluan tersebut adalah:

Mean + 0,25 SD

• Untuk mengelompokkan Raw Score (skor mentah) kedalam nilai yang berskala 3 atau huruf (A, B, dan C) patokan yang digunakan adalah;

A -1   =          > Mean + 1SD

B – 2  =          Mean + 1SD —– Mean – 1SD

C – 3  =          < Mean – 1SD

• Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 5 atau huruf (A, B, C, D, dan E) patokan yang digunakan adalah;

Mean + 1,5 SD

Mean + 0,5 SD

Mean – 1,5 SD

Mean – 0,5 SD

A -1   =          > Mean + 1,5 SD

B – 2  =          Mean + 1,5 SD —– Mean + 0,5 SD

C – 3  =          Mean + 0,5 SD —– Mean – 0,5 SD

D – 4 =          Mean – 0,5 SD —– Mean – 1,5 SD

E – 5  =          <  Mean – 1,5 SD

• Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 10 atau huruf (A, B, C, D, E, F, G, H, I, dan J) patokan yang digunakan adalah;

A – 1 =          > Mean + 1,75 SD

B – 2 =          Mean + 1,75 SD —– Mean + 1,25 SD

C – 3 =          Mean + 1,25 SD —– Mean + 0,75 SD

D – 4 =          Mean + 0,75 SD —– Mean + 0,25 SD

E – 5 =          Mean + 0,25 SD —– Mean +  SD

F – 6  =          Mean + SD —– Mean – 0,25 SD

G – 7 =          Mean – 0,25 SD —– Mean – 0,75 SD

H – 8 =          Mean – 0,75 SD  —– Mean – 1,25 SD

I – 9  =          Mean – 1,25 SD  —– Mean – 1,75 SD

J – 10            =          < Mean – 1,75 SD

 

Angka Baku

• Z score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. Z skor mempunyai dua bagian : (a) tanda (bisa positif atau negatif), (b) nilai numerik. Kondisi di atas rata-rata diberi tanda positif dan kondisi di bawah rata-rata diberi tanda negatif. Nilai numerik Z skor diperoleh dari perbedaan antara nilai asli dengan rata-ratanya dibagi dengan simpangan baku.

Angka baku adalah ukuran penyimpangan data dari rata-rata.

• z dapat bernilai nol (0), positif (+) atau negatif ( -)
• z nol → data bernilai sama dengan rata-rata populasi
• z positif → data bernilai di atas rata-rata populasi
• z negatif → data bernilai di bawah rata-rata

Untuk Mengubah (menkonversikan) Raw Score Menjadi standar z (z Score) data diperoleh dengan Rumus

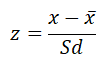
z           = Angka Baku

     = Rata-rata

Sd        = Simpangan Baku

 

• T-score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. T-score menggunakan rata-rata 50 dan Standar deviasi 10. Sehingga T-score dapat dicari dengan menggunakan rumus.

 

keterangan

+          →        Jika Sifat Data Berbanding Lurus

–           →        Jika Sifat Data Berbanding Terbalik

       = Rata-rata

Sd        = Simpangan Baku

Penyusunan data yang telah disusun dari yang terkecil sampai yang terbesar atau sebaliknya, bukan berarti bahwa penyederhanaan data tersebut telah selesai. Jika jumlah responden yang diteliti banyak, maka barisan data yang tersusun pun akan panjang. Keadaan ini masih belum membantu peneliti dalam mengamati data tersebut. Agar data tersebut lebih sederhana maka perlu dibuat suatu distribusi frekuensi yaitu mengumpulkan data yang sama dalam satu kelompok. Dengan demikian dibutuhkan cara penyajian data dengan cara membuat distribusi data melalui pembuatan daftar distribusi frekuensi. Daftar distribusi frekuensi adalah penyusunan urutan data ke dalam kelas-kelas interval, untuk kemudian ditentukan jumlah frekuensinya berdasarkan data yang sesuai dengan batas-batas interval kelasnya. Distribusi frekuensi ada bermacam-macam, di antaranya :

Ditinjau dari nyata tidaknya frekuensi

• Distribusi Frekuensi Absolut

Distribusi frekuensi absolut adalah suatu jumlah bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu. Distribusi ini disusun berdasar apa adanya, sehingga tidak menyukarkan peneliti dalam membuat distribusi ini.

• Distribusi Frekuensi Relatif

Merupakan suatu jumlah persentase yang menyatakan banyaknya data pada suatu kelompok tertentu.

Tahap penyusunan data menjadi daftar distribusi frekuensi antara lain adalah:

• Menghitung jumlah data
• Mencari data tertinggi dan terendah
• Menetapkan range
•  
• Merencanakan jumlah kelas

Jumlah kelas dihitung dengan menggunakan kaedah Sturges:

dimana n adalah jumlah data

5. Menentukan panjang kelas

Panjang kelas ditentukan dengan persamaan berikut:

6. Menentukan ujung bawah pada kelas interval

Ujung bawah kelas interval ditentukan dengan cara menjumlahkan data terkecil yang ditetapkan sebagai ujung bawah kelas interval pertama dengan nilai panjang kelas (p).

7. Menetapkan nilai ujung atas kelas interval

Ujung atas kelas interval dimulai dengan interval kelas pertama sampai dengan kelas terakhir.

1. Jika ujung-ujung bawah adalah bilangan bulat, maka nilai-nilai dari ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai selisih 1 dengan nilai ujung bawah berikutnya.
2. Jika ujung-ujung bawah adalah bilangan 1 desimal, maka nilai ujung-ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai seliisih 0,1 dengan nilai ujung bawah berikutnya.

8. Menentukan batas bawah dan batas atas kelas interval

9. Menentukan nilai tengah

Nilai tengah dapat ditentuan sebagai berikut:

10. Frekuensi

Banyak data dalam setiap interval kelas yang diperoleh dari himpunan data disesuaikan dengan batas-batas interval kelas.

Adapun macam-macam distribusi frekuensi adalah:

1. Distribusi frekuensi relatif

Distribusi frekuensi relatif dapat dinyatakan dalam bentuk relatif (persentase). Frekuensi relatif kadang-kadang dinyatakan dalam bentuk perbandingan ataupun desimal.

Contoh 2.4:

Misalkan jumlah seluruh data adalah 125, maka diperolehdiperoleh tabel distribusi berikut ini:

Tabel 2.1 Distribusi frekuensi relatif dari Contoh 2.4

• Distribusi frekuensi kumulatif

Distribusi frekuensi kumulatif adalah distribusi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlahkan. Ada dua macam distribusi frekuensi kumulatif, yaitu distribusi frekuensi kumulatif kurang dari dan lebih dari.

1. Distribusi Frekuensi Kumulatif kurang dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.
2. Distribusi Frekuensi Kumulatif lebih dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.

Contoh 2.5:

Berikut ini adalah data 50 mahasiswa dalam perolehan nilai statistik pada Prodi Pendidikan Olaharaga dan Kesehatan pada Universitas “T” semester V tahun 2015:

Nyatakan data-data tersebut ke dalam bentuk tabel distribusi frekuensi kurang dari dan lebih dari!

Penyelesaian:

Tabel 3.2 Tabel distribusi frekuensi kurang dari dan lebih dari

(a) Tabel distribusi frekuensi kumulatif kurang dari

(b) Tabel distribusi frekuensi kumulatif lebih dari

Contoh Soal 2.1:

Misalkan terdapat sekelompok data berikut ini:

10	20	14	15	21	25	27	15	13	12
17	14	16	28	22	21	22	23	25	20

Kelompokkan data-data tersebut ke dalam suatu distribusi frekuensi!

 PENYAJIAN DATA

Secara garis besar ada dua cara penyajian data yaitu dengan tabel dan grafik. Dua cara penyajian data ini saling berkaitan karena pada dasarnya sebelum dibuat grafik data tersebut berupa tabel. Penyajian data berupa grafik lebih komunikatif.

1. Penyajian data dengan tabel

Tabel atau daftar merupakan kumpulan angka yang disusun menurut kategori atau karakteristik data sehingga memudahkan untuk analisis data.

Ada tiga jenis tabel yaitu :

1. Tabel satu arah atau satu komponen adalah tabel yang hanya terdiri atas satu kategori atau karakteristik data. Tabel berikut ini adalah contoh tabel satu arah.

Banyaknya Pegawai Negeri Sipil Menurut Golongan Tahun 1990

Sumber : BAKN, dlm Statistik Indonesia, 1986

2. Tabel dua arah atau dua komponen adalah tabel yang menunjukkan dua kategori atau dua karakteristik. Tabel berikut ini adalah contoh tabel dua arah.

 Jumlah Mahasiswa UNP menurut Fakultas dan Kewarganegaraan 1995

Sumber : BAAK UNP, 2010

3. Tabel tiga arah atau tiga komponen adalah tabel yang menunjukkan tiga kategori atau tiga karakteristik. Contoh tabel berikut ini.

 Jumlah Pegawai Menurut Golongan, Umur dan Pendidikan pada Departeman A Tahun 2000

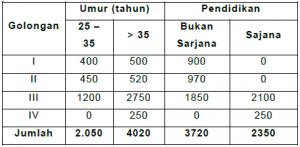
Sumber : Data Buatan

1. Penyajian data dengan grafik/diagram

Penyajian distribusi frekuensi biasanya dalam bentuk grafik. Grafik merupakan gambar-gambar yang menunjukkan data secara visual yang biasanya dibuat berdasarkan nilai pengamatan aslinya ataupun dari tabel-tabel sebelumnya. Keuntungan menggunakan grafik yaitu:

1. Grafik lebih mudah diingat daripada tabel
2. grafik menarik bagi orang-orang tertentu yang tidak menyukai angka dan tabel
3. dapat diperoleh informasi secara visual dan juga dapat digunakan untuk membandingkan secara visual pula
4. dapat menunjukkan perubahan hubungan satu bagian dalam rangka data dengan bagian yang lainnya.

Terdapat beberapa jenis grafik yaitu :

1. Grafik garis (line chart)

Grafik garis atau diagram garis dipakai untuk menggambarkan data berkala. Grafik garis dapat berupa grafik garis tunggal maupun grafik garis berganda.

1. Grafik batang / balok (bar chart)

Grafik batang pada dasarnya sama fugsinya dengan grafik garis yaitu untuk menggambarkan data berkala. Grafik batang juga terdiri dari grafik batang tunggal dan grafik batang ganda.

1. Grafik lingkaran (pie chart)

Grafik lingkaran lebih cocok untuk menyajikan data cross section, dimana data tersebut dapat dijadikan bentuk prosentase.

1. UKURAN NILAI PUSAT

Ukuran pemusatan adalah sembarang ukuran yang menunjukkan pusat segugus data yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya

1. Data yang tidak dikelompokkan

Adalah data yang berdiri sendiri secara numerik berdasarkan data apa adanya.

1. Mean

Mean atau rata-rata merupakan hasil bagi dari sejumlah skor dengan banyaknya responden. Perhitungan mean merupakan perhitungan yang sederhana karena hanya membutuhkan jumlah skor dan jumlah responden (n). Jika pencaran skor berdistribusi normal, maka rata-rata skor merupakan nilai tengah dari distribusi frekuensi skor tersebut. Rata-rata tidak mempertimbangkan pencaran (variabilitas) skor, sehingga sebelum melakukan interpretasi atas nilai rata-rata perlu melihat variabilitasnya.

Cara Mencari Mean

Untuk data tunggal

untuk data berkelompok

x : rata-rata hitung populasi

xi            : data ke-I (untuk data tunggal)

xi            : nilai tengah (untuk data kelompok)

f             : banyak data

Sedangkan mencari mean untuk data interval menggunakan rumus:

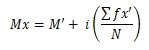
Mx = Mean

Mʹ = Mean Terkaan atau Mean Taksiran

i = Interval Kelas

Σfxʹ = jumlah perkalian titik tengah buatan sendiri dengan frekuensi dari masing-masing interval

N = Banyak Sampel

 

1. Median

Median merupakan skor yang membagi distribusi frekuensi menjadi dua sama besar. Langkah awal menentukan median adalah menyusun data menjadi bentuk tersusun menurut besarnya. Baru kemudian ditentukan nilai tengahnya (skor yang membagi distribusi menjadi dua sama besar). Jika jumlah frekuensi ganjil, maka nementukan median akan mudah yaitu skor yang terletak di tengah-tengah barisan skor. Apabila jumlah frekuensi genap, maka median merupakan rata-rata dari dua skor yang paling dekat dengan median. Median merupakan segugus data yang telah diurutkan dari yang terkecil sampai terbesar atau terbesar sampai terkecil yang tepat ditengah-tengahnya bila pengamatan itu ganjil, atau rata-rata kedua pengamatan yang ditengah bila pengamatannya genap maka:

Jika banyak data (n) ganjil dan tersortir, maka:

Jika banyak data (n) genap dan tersortir, maka:

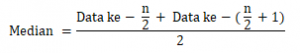
Untuk data interval menggunakan Rumus:

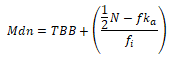
Mdn    = median

TBB    = low limit atau Tepi batas bawah

fi          = frekuensi kelas median

fk_a          = frekuensi kumulatif yang terletak diatas interval yang mengandung median

N         = banyak data

1. Modus

Merupakan nilai yang paling sering muncul atau dengan frekuensi yang paling tinggi. Modus tidak selalu ada, ini terjadi jika frekuensi semua data sama. Modus juga dapat lebih dari satu, jika terdapat lebih dari satu frekuensi tertinggi yang sama dan dikatakan sebagai bimodus.

Untuk menentukan modus dengan data interval

M_o       = Modus

TBB    = low lomit atau tepi batas bawah

fk_a          = frekuensi kumulatif yang terletak di atas interval yang mengandung modus

fk_b         = frekuensi kumulatif yang terletak di bawah interval yang mengandung modus

UKURAN LETAK

Individu skor atau nilai X disebut dengan raw score. Raw Score tidak dapat memberi informasi yang banyak, untuk itu perlu suatu perhitungan yang akan bermanfaat dalam menginterpretasikan skor yang terkumpul. Suatu contoh Nilai Praktek Lapangan mahasiswa A adalah 70, dalam hal ini si A tidak dapat mengatakan apa-apa tentang nilainya kecuali hanya menyebutkan besarnya nilai. Untuk mengevaluasi skor tersebut perlu banyak informasi seperti rata-rata kelas atau berapa banyak teman-temannya yang memperoleh nilai di bawahnya, sama dengannya, maupun di atasnya.

Frekuensi distribusi dapat dikelompok-kelompokkan menjadi beberapa bagian yang sama besar, pengelompokkan tersebut dapat dilakukan dengan : Quartile, Decile, dan Precentile.

1. Kuartil

Kuartil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 4 bagian yang sama besar.

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Kuartil ke-1 = n/4

Letak Kuartil ke-2 =  2n/4 = n/2 =  Letak Median

Letak Kuartil ke-3 = 3n/4

Dimana :

n                               : banyak data

Kelas Kuartil ke-q   : Kelas di mana Kuartil ke-q berada

Kelas Kuartil ke-q didapatkan dengan membandingkan Letak Kuartil ke-q dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

q          : 1,2 dan 3

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sebelum kelas Kuartil ke-q

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Kuartil ke-q

i           : interval kelas

f q        : Frekuensi kelas Kuartil ke-q

 

2. Desil

Desil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 10 bagian yang sama besar

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Desil ke-1 = n/10

Letak Desil ke-5 = 5n/10 = n/2 = Letak Median

Letak Desil ke-9 = 9n/10

Dimana:

n                      : banyak data

Kelas Desil ke-d          : Kelas di mana Desil ke-d berada

Kelas Desil ke-d didapatkan dengan membandingkan Letak Desil ke-d dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

d          : 1-9

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Desil ke-d dengan Frekuensi Kumulatif sebelum kelas Desil ke-d

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Desil ke-d

p          : panjang interval

f d        : Frekuensi kelas Desil ke-d

 

3. Persentil

Persentil adalah nilai yang membagi gugus data yang telah tersortir (ascending) menjadi 100 bagian yang sama besar

Untuk Data Tunggal dapat menggunakan Rumus:

Letak Persentil ke-1 = n/100

Letak Persentil ke-50 = 50n/100 = n/2 =  Letak Median

Letak Persentil ke-99 = 99n/100

Dimana:

n                      : banyak data

Kelas Persentil ke-p     : Kelas di mana Persentil ke-p berada

Kelas Persentil ke-p didapatkan dengan membandingkan Letak Persentil ke-p dengan Frekuensi Kumulatif

Untuk Data Bergolong dapat menggunakan Rumus:

di mana :

p          : 1-99

TBB     : Tepi Batas Bawah

s           : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sebelum kelas Persentil ke-p

TBA    : Tepi Batas Atas

s’         : selisih antara Letak Kuartil ke-q dengan Frekuensi Kumulatif sampai kelas Persentil ke-p

i           : interval kelas

f q        : Frekuensi kelas Kuartil ke-q

 

 

Silahkan tinggalkan pertanyaan pada menu “coment”

penerapan media blog dalam perkuliahan