Standar Deviasi dan Varians
UKURAN PENYEBARAN
Ragam dan Simpangan Baku untuk Data tidak Dikelompokkan
- Simpangan baku, paling sering digunakan untuk mengukur penyebaran. Nilai simpangan baku menunjukkan seberapa dekat nilai-nilai suatu data dengan nilai rata-rata.
- Nilai simpangan baku yang kecil → data menyebar dalam range lebih kecil mendekati nilai rata-rata mean, dan begitu sebaliknya.
- Nilai simpangan baku diperoleh dari akar kuadrat nilai ragam (varians)
- Ragam dari suatu data populasi dinotasikan sebagai σ², sedangkan untuk data sampel dinotasikan sebagai s².
- Simpangan baku σ (untuk data populasi), dan simpangan baku s (untuk data sampel)
adapun rumus standar Deviasi

Deviasi standar dan mean merupakan ukuran statistik yang memiliki reliabilitas yang tinggi sehinga dapat digunakan sbagai alat untuk evaluasi. Sebagai contoh dalam dunia pendididkan dapat digunaka sebagai alat evaluasi hasil belajar anak peserta didik. Cara yang sering digunakan sebagai bahan evalausi adalah sebagai berikut;
- Untuk menetapkan Nilai Batas Lulus Aktual (Minimum Passing Level atau Passing Grade), nilai yang digunakan sebagai acuan untuk keperluan tersebut adalah:
Mean + 0,25 SD
- Untuk mengelompokkan Raw Score (skor mentah) kedalam nilai yang berskala 3 atau huruf (A, B, dan C) patokan yang digunakan adalah;
A -1 = > Mean + 1SD
B – 2 = Mean + 1SD —– Mean – 1SD
C – 3 = < Mean – 1SD
- Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 5 atau huruf (A, B, C, D, dan E) patokan yang digunakan adalah;
Mean + 1,5 SD
Mean + 0,5 SD
Mean – 1,5 SD
Mean – 0,5 SD
A -1 = > Mean + 1,5 SD
B – 2 = Mean + 1,5 SD —– Mean + 0,5 SD
C – 3 = Mean + 0,5 SD —– Mean – 0,5 SD
D – 4 = Mean – 0,5 SD —– Mean – 1,5 SD
E – 5 = < Mean – 1,5 SD
- Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 10 atau huruf (A, B, C, D, E, F, G, H, I, dan J) patokan yang digunakan adalah;
A – 1 = > Mean + 1,75 SD
B – 2 = Mean + 1,75 SD —– Mean + 1,25 SD
C – 3 = Mean + 1,25 SD —– Mean + 0,75 SD
D – 4 = Mean + 0,75 SD —– Mean + 0,25 SD
E – 5 = Mean + 0,25 SD —– Mean + SD
F – 6 = Mean + SD —– Mean – 0,25 SD
G – 7 = Mean – 0,25 SD —– Mean – 0,75 SD
H – 8 = Mean – 0,75 SD —– Mean – 1,25 SD
I – 9 = Mean – 1,25 SD —– Mean – 1,75 SD
J – 10 = < Mean – 1,75 SD
Angka Baku
- Z score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. Z skor mempunyai dua bagian : (a) tanda (bisa positif atau negatif), (b) nilai numerik. Kondisi di atas rata-rata diberi tanda positif dan kondisi di bawah rata-rata diberi tanda negatif. Nilai numerik Z skor diperoleh dari perbedaan antara nilai asli dengan rata-ratanya dibagi dengan simpangan baku.
Angka baku adalah ukuran penyimpangan data dari rata-rata.
- z dapat bernilai nol (0), positif (+) atau negatif ( -)
- z nol → data bernilai sama dengan rata-rata populasi
- z positif → data bernilai di atas rata-rata populasi
- z negatif → data bernilai di bawah rata-rata
Untuk Mengubah (menkonversikan) Raw Score Menjadi standar z (z Score) data diperoleh dengan Rumus
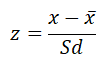
z = Angka Baku
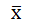 = Rata-rata
= Rata-rata
Sd = Simpangan Baku
- T-score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. T-score menggunakan rata-rata 50 dan Standar deviasi 10. Sehingga T-score dapat dicari dengan menggunakan rumus.
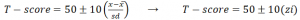
keterangan
+ → Jika Sifat Data Berbanding Lurus
– → Jika Sifat Data Berbanding Terbalik
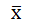 = Rata-rata
= Rata-rata
Sd = Simpangan Baku
Be the First to comment.
UKURAN PENYEBARAN
Ragam dan Simpangan Baku untuk Data tidak Dikelompokkan
- Simpangan baku, paling sering digunakan untuk mengukur penyebaran. Nilai simpangan baku menunjukkan seberapa dekat nilai-nilai suatu data dengan nilai rata-rata.
- Nilai simpangan baku yang kecil → data menyebar dalam range lebih kecil mendekati nilai rata-rata mean, dan begitu sebaliknya.
- Nilai simpangan baku diperoleh dari akar kuadrat nilai ragam (varians)
- Ragam dari suatu data populasi dinotasikan sebagai σ², sedangkan untuk data sampel dinotasikan sebagai s².
- Simpangan baku σ (untuk data populasi), dan simpangan baku s (untuk data sampel)
adapun rumus standar Deviasi

Deviasi standar dan mean merupakan ukuran statistik yang memiliki reliabilitas yang tinggi sehinga dapat digunakan sbagai alat untuk evaluasi. Sebagai contoh dalam dunia pendididkan dapat digunaka sebagai alat evaluasi hasil belajar anak peserta didik. Cara yang sering digunakan sebagai bahan evalausi adalah sebagai berikut;
- Untuk menetapkan Nilai Batas Lulus Aktual (Minimum Passing Level atau Passing Grade), nilai yang digunakan sebagai acuan untuk keperluan tersebut adalah:
Mean + 0,25 SD
- Untuk mengelompokkan Raw Score (skor mentah) kedalam nilai yang berskala 3 atau huruf (A, B, dan C) patokan yang digunakan adalah;
A -1 = > Mean + 1SD
B – 2 = Mean + 1SD —– Mean – 1SD
C – 3 = < Mean – 1SD
- Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 5 atau huruf (A, B, C, D, dan E) patokan yang digunakan adalah;
Mean + 1,5 SD
Mean + 0,5 SD
Mean – 1,5 SD
Mean – 0,5 SD
A -1 = > Mean + 1,5 SD
B – 2 = Mean + 1,5 SD —– Mean + 0,5 SD
C – 3 = Mean + 0,5 SD —– Mean – 0,5 SD
D – 4 = Mean – 0,5 SD —– Mean – 1,5 SD
E – 5 = < Mean – 1,5 SD
- Untuk mengubah Raw Score (skor mentah) kedalam nilai yang berskala 10 atau huruf (A, B, C, D, E, F, G, H, I, dan J) patokan yang digunakan adalah;
A – 1 = > Mean + 1,75 SD
B – 2 = Mean + 1,75 SD —– Mean + 1,25 SD
C – 3 = Mean + 1,25 SD —– Mean + 0,75 SD
D – 4 = Mean + 0,75 SD —– Mean + 0,25 SD
E – 5 = Mean + 0,25 SD —– Mean + SD
F – 6 = Mean + SD —– Mean – 0,25 SD
G – 7 = Mean – 0,25 SD —– Mean – 0,75 SD
H – 8 = Mean – 0,75 SD —– Mean – 1,25 SD
I – 9 = Mean – 1,25 SD —– Mean – 1,75 SD
J – 10 = < Mean – 1,75 SD
Angka Baku
- Z score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. Z skor mempunyai dua bagian : (a) tanda (bisa positif atau negatif), (b) nilai numerik. Kondisi di atas rata-rata diberi tanda positif dan kondisi di bawah rata-rata diberi tanda negatif. Nilai numerik Z skor diperoleh dari perbedaan antara nilai asli dengan rata-ratanya dibagi dengan simpangan baku.
Angka baku adalah ukuran penyimpangan data dari rata-rata.
- z dapat bernilai nol (0), positif (+) atau negatif ( -)
- z nol → data bernilai sama dengan rata-rata populasi
- z positif → data bernilai di atas rata-rata populasi
- z negatif → data bernilai di bawah rata-rata
Untuk Mengubah (menkonversikan) Raw Score Menjadi standar z (z Score) data diperoleh dengan Rumus
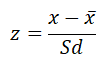
z = Angka Baku
![]() = Rata-rata
= Rata-rata
Sd = Simpangan Baku
- T-score merupakan perbedaan antara raw score (skor asli) dan rata-rata dengan menggunakan unit-unit simpangan baku untuk mengukur perbedaan. T-score menggunakan rata-rata 50 dan Standar deviasi 10. Sehingga T-score dapat dicari dengan menggunakan rumus.
![]()
keterangan
+ → Jika Sifat Data Berbanding Lurus
– → Jika Sifat Data Berbanding Terbalik
![]() = Rata-rata
= Rata-rata
Sd = Simpangan Baku
