DISTRIBUSI FREKUENSI
Penyusunan data yang telah disusun dari yang terkecil sampai yang terbesar atau sebaliknya, bukan berarti bahwa penyederhanaan data tersebut telah selesai. Jika jumlah responden yang diteliti banyak, maka barisan data yang tersusun pun akan panjang. Keadaan ini masih belum membantu peneliti dalam mengamati data tersebut. Agar data tersebut lebih sederhana maka perlu dibuat suatu distribusi frekuensi yaitu mengumpulkan data yang sama dalam satu kelompok. Dengan demikian dibutuhkan cara penyajian data dengan cara membuat distribusi data melalui pembuatan daftar distribusi frekuensi. Daftar distribusi frekuensi adalah penyusunan urutan data ke dalam kelas-kelas interval, untuk kemudian ditentukan jumlah frekuensinya berdasarkan data yang sesuai dengan batas-batas interval kelasnya. Distribusi frekuensi ada bermacam-macam, di antaranya :
Ditinjau dari nyata tidaknya frekuensi
- Distribusi Frekuensi Absolut
Distribusi frekuensi absolut adalah suatu jumlah bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu. Distribusi ini disusun berdasar apa adanya, sehingga tidak menyukarkan peneliti dalam membuat distribusi ini.
- Distribusi Frekuensi Relatif
Merupakan suatu jumlah persentase yang menyatakan banyaknya data pada suatu kelompok tertentu.
Tahap penyusunan data menjadi daftar distribusi frekuensi antara lain adalah:
- Menghitung jumlah data
- Mencari data tertinggi dan terendah
- Menetapkan range
-

- Merencanakan jumlah kelas
Jumlah kelas dihitung dengan menggunakan kaedah Sturges:

dimana n adalah jumlah data
- Menentukan panjang kelas
Panjang kelas ditentukan dengan persamaan berikut:

- Menentukan ujung bawah pada kelas interval
Ujung bawah kelas interval ditentukan dengan cara menjumlahkan data terkecil yang ditetapkan sebagai ujung bawah kelas interval pertama dengan nilai panjang kelas (p).
- Menetapkan nilai ujung atas kelas interval
Ujung atas kelas interval dimulai dengan interval kelas pertama sampai dengan kelas terakhir.
- Jika ujung-ujung bawah adalah bilangan bulat, maka nilai-nilai dari ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai selisih 1 dengan nilai ujung bawah berikutnya.
- Jika ujung-ujung bawah adalah bilangan 1 desimal, maka nilai ujung-ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai seliisih 0,1 dengan nilai ujung bawah berikutnya.
8. Menentukan batas bawah dan batas atas kelas interval
9. Menentukan nilai tengah
Nilai tengah dapat ditentuan sebagai berikut:

- Frekuensi
Banyak data dalam setiap interval kelas yang diperoleh dari himpunan data disesuaikan dengan batas-batas interval kelas.
Adapun macam-macam distribusi frekuensi adalah:
- Distribusi frekuensi relatif
Distribusi frekuensi relatif dapat dinyatakan dalam bentuk relatif (persentase). Frekuensi relatif kadang-kadang dinyatakan dalam bentuk perbandingan ataupun desimal.
Contoh 2.4:

Misalkan jumlah seluruh data adalah 125, maka diperolehdiperoleh tabel distribusi berikut ini:
Tabel 2.1 Distribusi frekuensi relatif dari Contoh 2.4

- Distribusi frekuensi kumulatif
Distribusi frekuensi kumulatif adalah distribusi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlahkan. Ada dua macam distribusi frekuensi kumulatif, yaitu distribusi frekuensi kumulatif kurang dari dan lebih dari.
- Distribusi Frekuensi Kumulatif kurang dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.
- Distribusi Frekuensi Kumulatif lebih dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.
Contoh 2.5:
Berikut ini adalah data 50 mahasiswa dalam perolehan nilai statistik pada Prodi Pendidikan Olaharaga dan Kesehatan pada Universitas “T” semester V tahun 2015:

Nyatakan data-data tersebut ke dalam bentuk tabel distribusi frekuensi kurang dari dan lebih dari!
Penyelesaian:
Tabel 3.2 Tabel distribusi frekuensi kurang dari dan lebih dari
(a) Tabel distribusi frekuensi kumulatif kurang dari

(b) Tabel distribusi frekuensi kumulatif lebih dari

Contoh Soal 2.1:
Misalkan terdapat sekelompok data berikut ini:
10
20
14
15
21
25
27
15
13
12
17
14
16
28
22
21
22
23
25
20
Kelompokkan data-data tersebut ke dalam suatu distribusi frekuensi!
PENYAJIAN DATA
Secara garis besar ada dua cara penyajian data yaitu dengan tabel dan grafik. Dua cara penyajian data ini saling berkaitan karena pada dasarnya sebelum dibuat grafik data tersebut berupa tabel. Penyajian data berupa grafik lebih komunikatif.
- Penyajian data dengan tabel
Tabel atau daftar merupakan kumpulan angka yang disusun menurut kategori atau karakteristik data sehingga memudahkan untuk analisis data.
Ada tiga jenis tabel yaitu :
- Tabel satu arah atau satu komponen adalah tabel yang hanya terdiri atas satu kategori atau karakteristik data. Tabel berikut ini adalah contoh tabel satu arah.
Banyaknya Pegawai Negeri Sipil Menurut Golongan Tahun 1990

Sumber : BAKN, dlm Statistik Indonesia, 1986
- Tabel dua arah atau dua komponen adalah tabel yang menunjukkan dua kategori atau dua karakteristik. Tabel berikut ini adalah contoh tabel dua arah.
Jumlah Mahasiswa UNP menurut Fakultas dan Kewarganegaraan 1995

Sumber : BAAK UNP, 2010
- Tabel tiga arah atau tiga komponen adalah tabel yang menunjukkan tiga kategori atau tiga karakteristik. Contoh tabel berikut ini.
Jumlah Pegawai Menurut Golongan, Umur dan Pendidikan pada Departeman A Tahun 2000
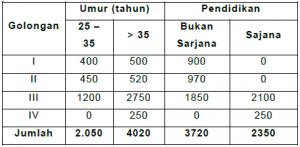
Sumber : Data Buatan
- Penyajian data dengan grafik/diagram
Penyajian distribusi frekuensi biasanya dalam bentuk grafik. Grafik merupakan gambar-gambar yang menunjukkan data secara visual yang biasanya dibuat berdasarkan nilai pengamatan aslinya ataupun dari tabel-tabel sebelumnya. Keuntungan menggunakan grafik yaitu:
- Grafik lebih mudah diingat daripada tabel
- grafik menarik bagi orang-orang tertentu yang tidak menyukai angka dan tabel
- dapat diperoleh informasi secara visual dan juga dapat digunakan untuk membandingkan secara visual pula
- dapat menunjukkan perubahan hubungan satu bagian dalam rangka data dengan bagian yang lainnya.
Terdapat beberapa jenis grafik yaitu :
- Grafik garis (line chart)
Grafik garis atau diagram garis dipakai untuk menggambarkan data berkala. Grafik garis dapat berupa grafik garis tunggal maupun grafik garis berganda.

- Grafik batang / balok (bar chart)
Grafik batang pada dasarnya sama fugsinya dengan grafik garis yaitu untuk menggambarkan data berkala. Grafik batang juga terdiri dari grafik batang tunggal dan grafik batang ganda.

- Grafik lingkaran (pie chart)
Grafik lingkaran lebih cocok untuk menyajikan data cross section, dimana data tersebut dapat dijadikan bentuk prosentase.

Be the First to comment.
Penyusunan data yang telah disusun dari yang terkecil sampai yang terbesar atau sebaliknya, bukan berarti bahwa penyederhanaan data tersebut telah selesai. Jika jumlah responden yang diteliti banyak, maka barisan data yang tersusun pun akan panjang. Keadaan ini masih belum membantu peneliti dalam mengamati data tersebut. Agar data tersebut lebih sederhana maka perlu dibuat suatu distribusi frekuensi yaitu mengumpulkan data yang sama dalam satu kelompok. Dengan demikian dibutuhkan cara penyajian data dengan cara membuat distribusi data melalui pembuatan daftar distribusi frekuensi. Daftar distribusi frekuensi adalah penyusunan urutan data ke dalam kelas-kelas interval, untuk kemudian ditentukan jumlah frekuensinya berdasarkan data yang sesuai dengan batas-batas interval kelasnya. Distribusi frekuensi ada bermacam-macam, di antaranya :
Ditinjau dari nyata tidaknya frekuensi
- Distribusi Frekuensi Absolut
Distribusi frekuensi absolut adalah suatu jumlah bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu. Distribusi ini disusun berdasar apa adanya, sehingga tidak menyukarkan peneliti dalam membuat distribusi ini.
- Distribusi Frekuensi Relatif
Merupakan suatu jumlah persentase yang menyatakan banyaknya data pada suatu kelompok tertentu.
Tahap penyusunan data menjadi daftar distribusi frekuensi antara lain adalah:
- Menghitung jumlah data
- Mencari data tertinggi dan terendah
- Menetapkan range
-

- Merencanakan jumlah kelas
Jumlah kelas dihitung dengan menggunakan kaedah Sturges:
![]()
dimana n adalah jumlah data
- Menentukan panjang kelas
Panjang kelas ditentukan dengan persamaan berikut:
![]()
- Menentukan ujung bawah pada kelas interval
Ujung bawah kelas interval ditentukan dengan cara menjumlahkan data terkecil yang ditetapkan sebagai ujung bawah kelas interval pertama dengan nilai panjang kelas (p).
- Menetapkan nilai ujung atas kelas interval
Ujung atas kelas interval dimulai dengan interval kelas pertama sampai dengan kelas terakhir.
- Jika ujung-ujung bawah adalah bilangan bulat, maka nilai-nilai dari ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai selisih 1 dengan nilai ujung bawah berikutnya.
- Jika ujung-ujung bawah adalah bilangan 1 desimal, maka nilai ujung-ujung atas pada interval kelas pertama, kedua dan seterusnya mempunyai seliisih 0,1 dengan nilai ujung bawah berikutnya.
8. Menentukan batas bawah dan batas atas kelas interval
9. Menentukan nilai tengah
Nilai tengah dapat ditentuan sebagai berikut:
![]()
- Frekuensi
Banyak data dalam setiap interval kelas yang diperoleh dari himpunan data disesuaikan dengan batas-batas interval kelas.
Adapun macam-macam distribusi frekuensi adalah:
- Distribusi frekuensi relatif
Distribusi frekuensi relatif dapat dinyatakan dalam bentuk relatif (persentase). Frekuensi relatif kadang-kadang dinyatakan dalam bentuk perbandingan ataupun desimal.
Contoh 2.4:

Misalkan jumlah seluruh data adalah 125, maka diperolehdiperoleh tabel distribusi berikut ini:
Tabel 2.1 Distribusi frekuensi relatif dari Contoh 2.4

- Distribusi frekuensi kumulatif
Distribusi frekuensi kumulatif adalah distribusi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlahkan. Ada dua macam distribusi frekuensi kumulatif, yaitu distribusi frekuensi kumulatif kurang dari dan lebih dari.
- Distribusi Frekuensi Kumulatif kurang dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.
- Distribusi Frekuensi Kumulatif lebih dari, adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.
Contoh 2.5:
Berikut ini adalah data 50 mahasiswa dalam perolehan nilai statistik pada Prodi Pendidikan Olaharaga dan Kesehatan pada Universitas “T” semester V tahun 2015:

Nyatakan data-data tersebut ke dalam bentuk tabel distribusi frekuensi kurang dari dan lebih dari!
Penyelesaian:
Tabel 3.2 Tabel distribusi frekuensi kurang dari dan lebih dari
(a) Tabel distribusi frekuensi kumulatif kurang dari

(b) Tabel distribusi frekuensi kumulatif lebih dari

Contoh Soal 2.1:
Misalkan terdapat sekelompok data berikut ini:
| 10 | 20 | 14 | 15 | 21 | 25 | 27 | 15 | 13 | 12 |
| 17 | 14 | 16 | 28 | 22 | 21 | 22 | 23 | 25 | 20 |
Kelompokkan data-data tersebut ke dalam suatu distribusi frekuensi!
PENYAJIAN DATA
Secara garis besar ada dua cara penyajian data yaitu dengan tabel dan grafik. Dua cara penyajian data ini saling berkaitan karena pada dasarnya sebelum dibuat grafik data tersebut berupa tabel. Penyajian data berupa grafik lebih komunikatif.
- Penyajian data dengan tabel
Tabel atau daftar merupakan kumpulan angka yang disusun menurut kategori atau karakteristik data sehingga memudahkan untuk analisis data.
Ada tiga jenis tabel yaitu :
- Tabel satu arah atau satu komponen adalah tabel yang hanya terdiri atas satu kategori atau karakteristik data. Tabel berikut ini adalah contoh tabel satu arah.
Banyaknya Pegawai Negeri Sipil Menurut Golongan Tahun 1990

Sumber : BAKN, dlm Statistik Indonesia, 1986
- Tabel dua arah atau dua komponen adalah tabel yang menunjukkan dua kategori atau dua karakteristik. Tabel berikut ini adalah contoh tabel dua arah.
Jumlah Mahasiswa UNP menurut Fakultas dan Kewarganegaraan 1995

Sumber : BAAK UNP, 2010
- Tabel tiga arah atau tiga komponen adalah tabel yang menunjukkan tiga kategori atau tiga karakteristik. Contoh tabel berikut ini.
Jumlah Pegawai Menurut Golongan, Umur dan Pendidikan pada Departeman A Tahun 2000

Sumber : Data Buatan
- Penyajian data dengan grafik/diagram
Penyajian distribusi frekuensi biasanya dalam bentuk grafik. Grafik merupakan gambar-gambar yang menunjukkan data secara visual yang biasanya dibuat berdasarkan nilai pengamatan aslinya ataupun dari tabel-tabel sebelumnya. Keuntungan menggunakan grafik yaitu:
- Grafik lebih mudah diingat daripada tabel
- grafik menarik bagi orang-orang tertentu yang tidak menyukai angka dan tabel
- dapat diperoleh informasi secara visual dan juga dapat digunakan untuk membandingkan secara visual pula
- dapat menunjukkan perubahan hubungan satu bagian dalam rangka data dengan bagian yang lainnya.
Terdapat beberapa jenis grafik yaitu :
- Grafik garis (line chart)
Grafik garis atau diagram garis dipakai untuk menggambarkan data berkala. Grafik garis dapat berupa grafik garis tunggal maupun grafik garis berganda.

- Grafik batang / balok (bar chart)
Grafik batang pada dasarnya sama fugsinya dengan grafik garis yaitu untuk menggambarkan data berkala. Grafik batang juga terdiri dari grafik batang tunggal dan grafik batang ganda.

- Grafik lingkaran (pie chart)
Grafik lingkaran lebih cocok untuk menyajikan data cross section, dimana data tersebut dapat dijadikan bentuk prosentase.

